前言
由于工作的原因,初次接触安全芯片并使用到安全相关的一些工具,并在后续的学习中陆陆续续看了一些安全的知识。在这里做一些security相关的笔记,希望之后可以温故知新,也希望能帮助到有需要的同学。
我主要参考了以下三本书籍,感兴趣的同学可以看看:
- 《图解密码技术》 :非常浅显易懂的入门书籍
- 《密码技术与物联网安全 – mbedtls开发实战》:19年出的mbedtls相关的书籍
- Understanding Cryptography, by Christo Paar
另外参考了别人的博文和维基百科,在此表示感谢:
单向散列函数
单项散列函数又称安全散列函数或哈希函数(Hash function),是一种从任何数据中创建小的数字“指纹”(fingerprint)的方法,可用于检查消息的完整性。
Motivation
在现代密码学中,哈希运算有着非常多的应用,最著名的是在数字签名中的运用。
在数字签名中,经常采用基于离散对数问题的非对称算法RSA算法,这种算法要求消息的长度不能比模数(modulus)小。实际常用的是模数长度是1024和3072-bits,而我们一封邮件就很可能比这个长度要大。
那么,怎么解决这种问题呢?
很容易想到的一种方法是,对消息分段,使得每段签名的长度,都比模数的长度小。
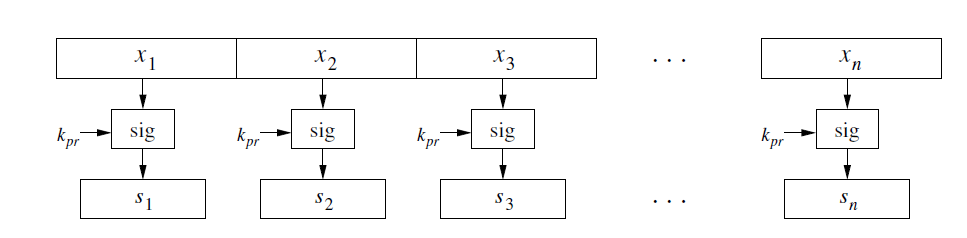
这种方法有什么坏处呢?
- 很大的运算负载。非对称的签名算法计算得很慢,全部计算效率太低。
- 长度太长。消息+签名,使得输出的长度直接变成了两倍。
- 安全的限制。攻击者从中截取掉部分消息和签名、对消息和签名变换顺序、重复消息和签名,都不会被发现。
因此,对消息进行分段加密使不可行的,在实际使用中,签名都是对消息的哈希(散列值)进行签名。首先,对完整的消息计算哈希值,然后再用签名算法对消息进行签名,这个哈希值,就代表了消息本身。消息的哈希值也常常叫做消息摘要(message digest)或者消息的指纹(fingerprint of the message)。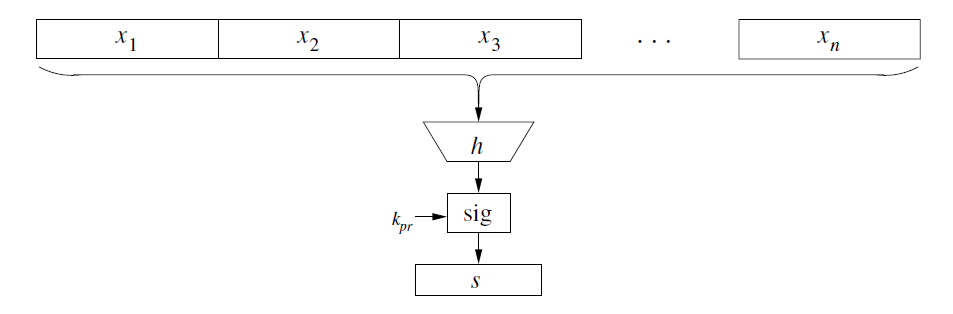
在讨论哈希的安全性之前,我们先总结一下哈希运算希望拥有的几个特性:
- 它能接受任意长度的消息输入,然后输出固定长度的哈希值(128-512bits)
- 这个哈希值跟输入的消息紧密相关(highly sensitive),输入做一点点小小的改变,哈希值都完全不一样。
- 运算尽量地快。
哈希函数的安全性要求
哈希函数跟加密算法不一样,哈希函数是不需要密钥的。为了保证哈希函数的安全,焊锡函数需要用有三个最主要的特性:
- 单向性(one-wayness)
- 抗弱碰撞性
- 抗强碰撞性
这三点特性描述如下图:
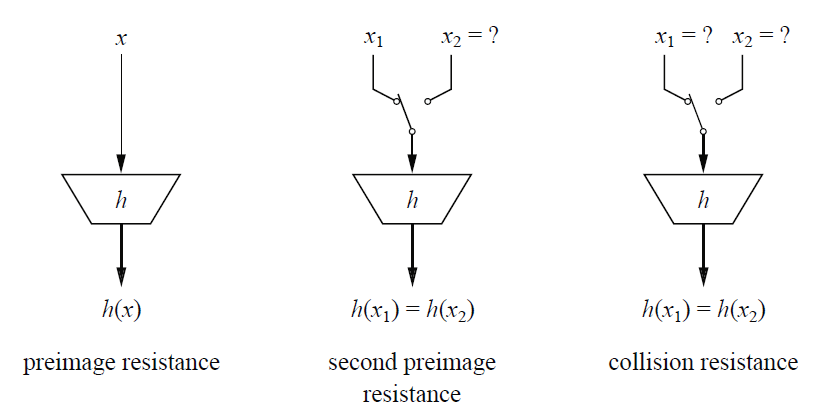
1 | 单向性:只能由输入计算输出,不能由输出反过来得到输入。 |
单向性
考虑一下为什么哈希函数需要具有单向性。我们假设Bob向Alice传输了加密的消息,以及(对明文哈希的)签名。
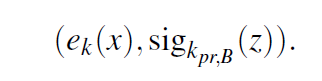
e()是对称加密算法,密钥是k。z是对明文的哈希,用Bob自己的公钥对z进行签名。
假设Bob用的是RSA签名算法,则签名由下式进行计算:
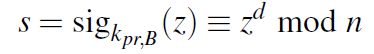
攻击这Oscar可以用Bob的公钥得到消息的哈希值:
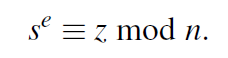
如果哈希函数不是单向的,那么通过z,就可以反过来得到明文x。而在这个传输中,Bob并不希望其他人知道明文。
此外,在哈希函数的另外一些应用中,比如密钥派生,单向性显得更为重要。
抗弱碰撞性
抗弱碰撞性很好理解,如果给定x1,能找到x2,使得它们得哈希值相等,则哈希值就不能作为消息的指纹了。

需要说明的是,由于我们输出的长度是有限的,根据鸽笼原理,100个笼子,101个鸽子,那么总是有1个笼子里面有不止一个鸽子。因此,我们指的抗弱碰撞性,是指的不能实现分析计算上的攻击,且穷举所有的可能,是不实际的。
抗强碰撞性
为什么需要抗强碰撞性呢?如果攻击者能修改x1,也能修改x2,那么并且能找到x1、x2的哈希值相等,那么攻击也同样能成为可能。
1 | x1: Transfer $10 into Oscar's acount |
过程如下:
1 | Oscar -> Bob:转10美元到我(Oscar)的账户 |

生日攻击
这里说明一下,抗强碰撞性的概率计算问题。
一年365天。366个人中,一定有至少2个人生日相同。但是如果我们想要求有两个人的生日相同的概率是50%,那么需要多少人呢?实际只需要23个人!
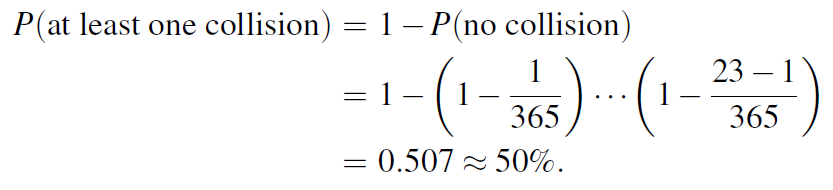
假设哈希函数的输出位数是n,碰撞的概率是lamda,输入尝试次数是t,它们之间存在关系:
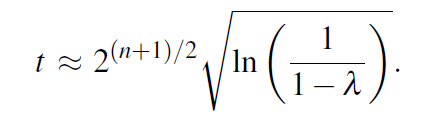
如果哈希函数输出长度是80位,碰撞概率是50%时,只需要尝试这么多次:
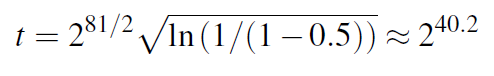
因此,所有的哈希函数,输出都至少有128位,有一些则会更多。
单向散列函数的应用
消息完整性检测
单向散列函数的一个重要应用是对消息的完整性进行检测。例如在传输消息的后面添加散列值,在传输完成之后再比较计算出来的散列值和收到的散列值是否相等,来检测是否发生了篡改。
伪随机数生成器
单向散列函数可以用来构造伪随机数生成算法,如TLS1.2中的PRF函数。
消息认证码
消息认证码用来检测消息传输过程中的错误、篡改和伪装。什么是伪装呢?比如Alice向Bob传输了一条带有散列值的消息,但是这个传输过程被Mallory截获,并且Mallory伪装成Alice发了一条新的消息+散列值给Bob。消息认证码就是为了完成认证的过程:它除了单项散列函数外还加入了共享密钥,该密钥只有Alice和Bob有,这样就能防止伪装,完成认证。
数字签名
因为“指纹”代表了数据的真实性,因此一般对“指纹”进行签名而不是对完整消息进行签名(太慢)。
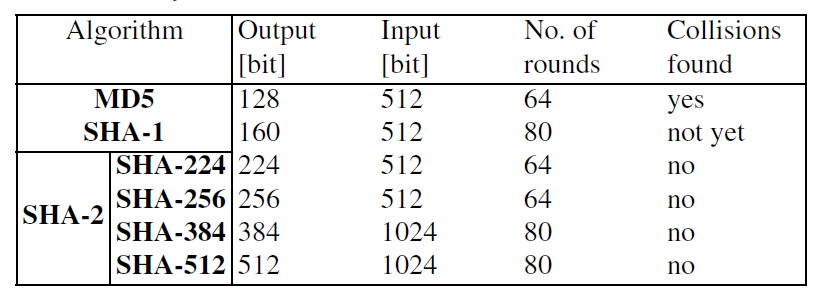
SHA256详细描述
单向散列函数的实现方法有很多种,常用的包括MD4、MD5、SHA-256、SHA384-512等。
MD4、MD5算法的碰撞性已被攻破,SHA0、SHA1算法存在缺陷不推荐使用,因此推荐使用的是SHA2和SHA3算法。
下面以SHA256为例详细描述哈希算法的计算过程。
常量初始化
首先介绍一下SHA256算法需要用到的常量以及逻辑运算。
SHA256算法使用到的8个哈希初值:
1 | (first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19): |
用到的64个常量:
1 | k[0..63] := |
需要到的逻辑运算
SHA256用到的逻辑运算包括:
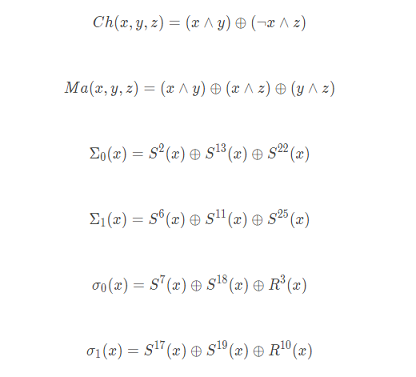
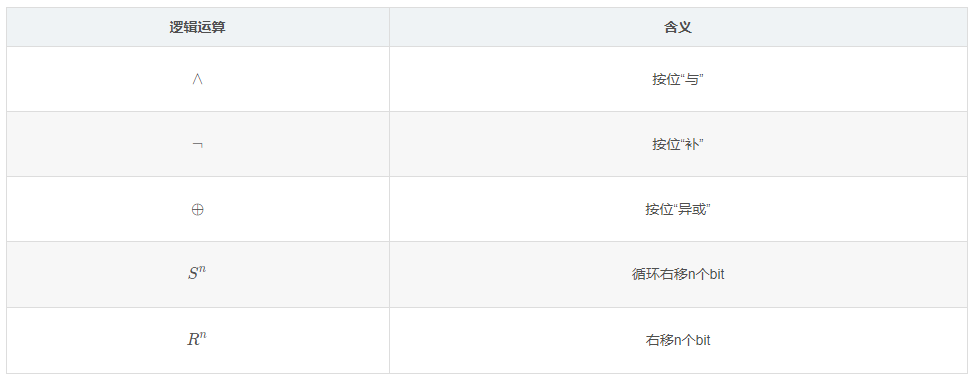
其中:
消息预处理
算法首先要对消息进行填充。
消息填充
SHA256算法的分组长度是512bit,因此需要先经过填充使长度达到512的整数倍。
假设原始数据长度是L比特,则在后面填充一个比特1、K个比特0和长度L的二进制表示(64比特)。K = (512 - 64 - 1 - L) mod 512
假设消息是”abc”,则填充后的消息为: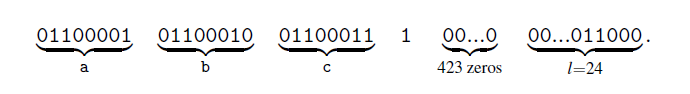
消息分割:
完成消息填充后,将消息M其分解成N个512比特的分组chunk: M(1)~M(N)。
哈希计算
计算哈希的过程,就是对消息进行N轮的映射计算的过程,表示为:
1 | H_i = Map(H_i-1, M(i)) //最外层循环,N轮 |
H_0是前面提到的8个哈希初值,利用Map映射函数对H进行更新,更新N轮后的输出H_N,就是最后的哈希值。
Map映射函数
首先,Map映射函数需要构造64个字(WORD)
每个512比特的分组消息M(i),可以用16个32比特表示:
w[0],...,w[15]
它们是64个字的前16个,后面的字由如下迭代公式的到:
w[t] = σ1(w[t-2]) + w[t-7] + σ0(w[t-15]) + w[t-16]
然后,Map映射包含了64次循环,每次循环的过程为:
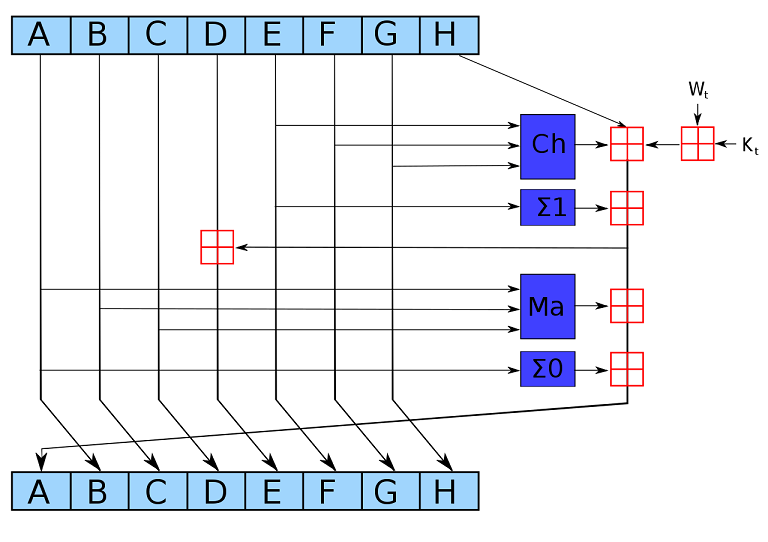
其中:
输入ABCDEFGH这8个字一开始的初值分别为:H_i-1(0),…,H_i-1(7),它们按照上图中的规则进行更新;
深蓝色方块是实现定义好的非线性逻辑函数;
红色田字方块表示:两个数字相加,对2^32求余;
Kt是第t个密钥,对应前面提到的64个常量;
Wt是本区块第t个word。
至此完成了SHA256的计算。